2. La construction du labyrinthe

Depuis longtemps j’étais intrigué par les jeux de ficelle (voir 3 Jeux de ficelle). Influencé par Levi-Strauss, qui suggère que les jeux de ficelle sont structurés comme les mythes, j’ai essayé de les déconstruire (fig. 17 et 18). Etonné par le résultat, je déconstruisais un nœud plus simple pour mieux comprendre le principe que j’appliquais. A ma grande surprise, en partant d’un nœud de cravate, je découvrais un dessin très semblable à celui du chemin du labyrinthe crétois.

 

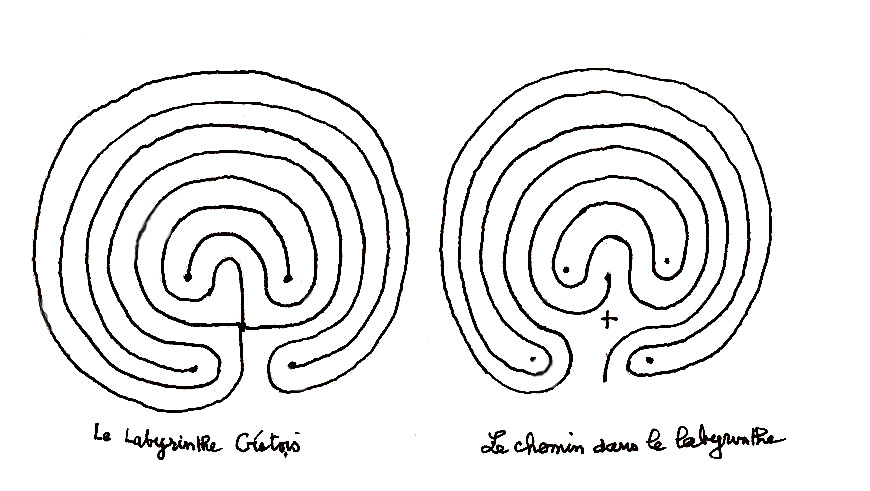
Fig. A

La méthode que je suivais consiste à transformer le fil du nœud en un axe et à suivre le parcours du fil recoupant cet axe (fig. B). Il suffisait alors de courber cet axe comme un colimaçon pour obtenir le dessin du labyrinthe (fig. C).

 

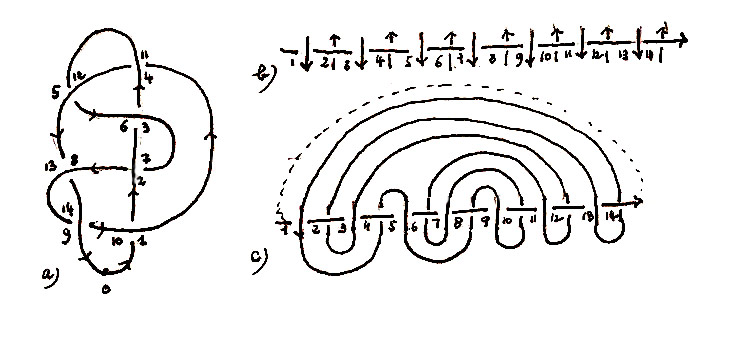
Fig. B

a) On oriente le fil du nœud et on numérote les croisements à partir de 0 en suivant le fil.
b) On transforme le fil en une ligne droite qui constitue un axe sur lequel les croisements sont numérotés.
c) On rejoint les croisements comme la corde du nœud l’indique, ce qui croise à 1 va croiser à 4 puis à 5, etc.
Le méandre présente alors un dessin qui rappelle celui du chemin dans le labyrinthe, si (fig C) on remplace l’axe
rectiligne par un colimaçon, on obtient le dessin original du chemin du labyrinthe crétois.

 

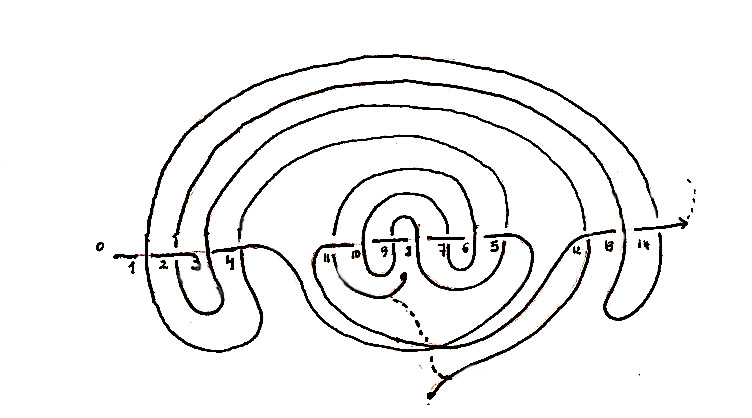
Fig. C

Le dessin du labyrinthe lorsque l'axe est replié comme un colimaçon

 

Les deux nouveaux croisements du méandre avec l’axe là où l’axe se replie tiennent au fait que l’observateur a tourné autour du nœud et que, à chaque fois qu’on passe de l’autre côté, on observe un croisement de plus. Ainsi on a cartographié le nœud complètement sous toutes ses faces. Comme pour la caverne de Platon, on obtient ainsi une vue plus complète et plus objective. Ce passage de l’autre côté est ce qui peut interrompre la continuité du méandre.

Bien sûr, ce procédé peut paraître artificiel, mais il suffisait d’imaginer que le nœud se déplaçait en suivant une double orbite pour que la lecture du nœud devienne logique (fig. D).

 

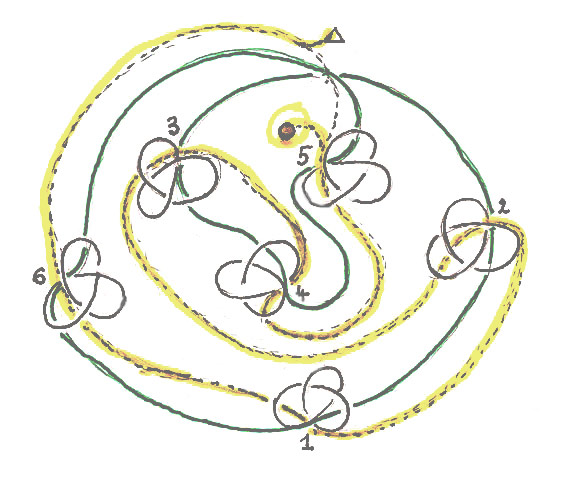
Fig. D

Pour montrer de manière simple le parcours du nœud, on utilisera un nœud simple qui lui aussi produit un petit labyrinthe marqué en jaune, mais le procédé est le même pour le nœud se croisant sept fois. On doit se souvenir que, entre 2 et 3 puis 5 et 6, l’observateur a tourné autour du nœud qui apparaît alors inversé.

 

Au lieu de décrire une déconstruction, le dessin du labyrinthe devient ainsi celui d’un mouvement (voir 4 Mouvement). Ce qui est surprenant, c’est cette correspondance entre, d’une part, une trajectoire et un mouvement extérieur et, d’autre part, une structure intérieure.
Pour obtenir le dessin du dédale il faut représenter le mouvement du nœud en entier. Lorsque le nœud tourne sur lui-même, comme le fait la Terre circulant autour du Soleil, le dédale devient assez complexe (fig. E).

 

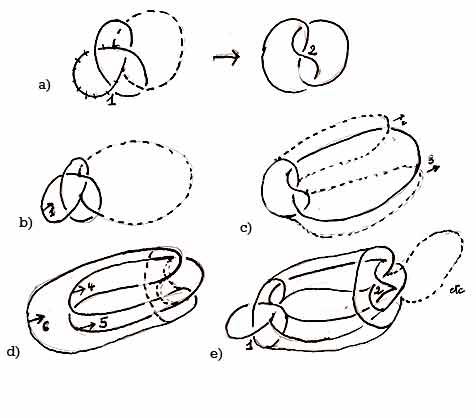
Fig. E

E-a : On peut montrer le spin du nœud en faisant basculer une boucle après l’autre. Pour aller de 1 à 2, une seule boucle du nœud bascule.
E-b,c,d,e : Mais il faut aussi montrer la translation du reste du nœud. Avec le nœud de cravate qui se croise sept fois, on obtient finalement un réseau assez complexe.

 

Finalement on peut comprendre comment, sans un fil d’Ariane, ce dédale peut devenir complètement inextricable. En effet sur la fig. F-a, on peut voir que le méandre allant de 1 à 2 peut aussi être considéré comme allant de 1, où il croise l’axe, à 5, sur l’axe. Si on mélange les deux systèmes, les nœuds se compliquent et se multiplient à l’infini (fig. F: b et c).

 

 

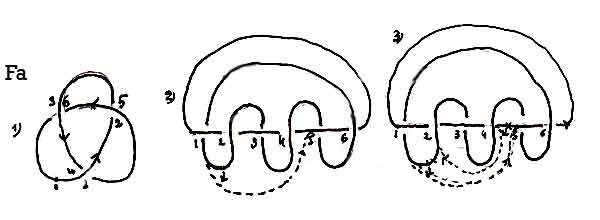
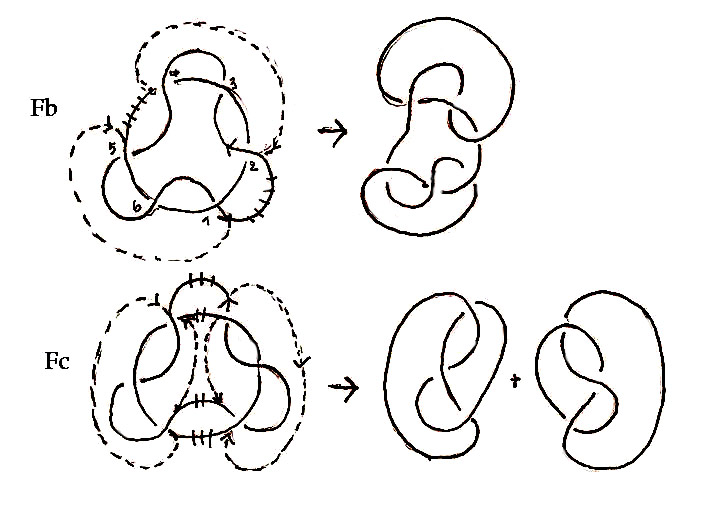
Lorsqu’on remplace un système par l’autre, il faut aussi remplacer le parcours de l’axe correspondant.
Si, par exemple, un parcours est remplacé, (Fig Fb) on obtient un nœud plus complexe que l’original.
Si deux parcours sont remplacés,(Fig Fc) on obtient deux nœuds semblables à l’original.