2. The construction of the labyrinth

 

For a long time I have been intrigued by the cat’s cradle (see 3 Cat’s Cradle). Influenced by Levi-Strauss who suggested that myths are structured on the same model as the cat’s cradle, I tried to unravel them. Puzzled by the results, I unravelled more simple knots in order to better understand the principle I was applying. To my great surprise, with the knot of a man’s tie, itself symbolic, I discovered a design very similar to the path of the labyrinth of Crete.

 

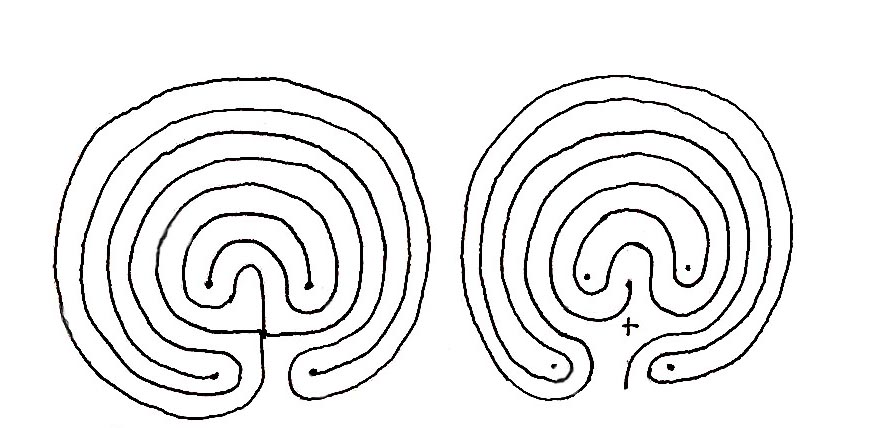
The Crete Labyrinth                                                             The Path in the labyrinth

Fig. A

The method I used consisted of transforming the knotted string into a straight line which then became an axis. Then I followed the path of the thread crossing this axis, (Fig B). It was then enough to curve this axis like a snail to obtain the drawing of the labyrinth (Fig C).

 

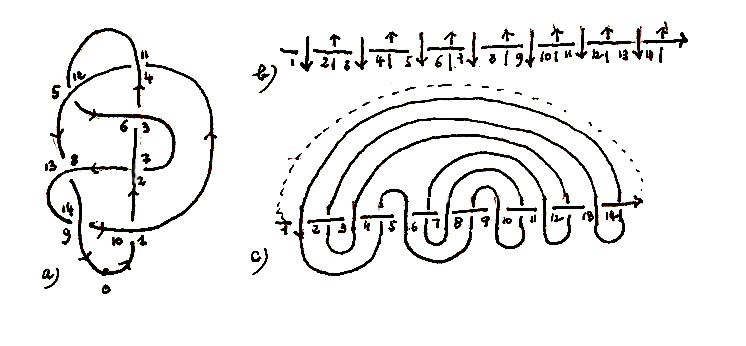
Fig. B

a)One orients the knotted thread and numbers the crossings , beginning from 0, while following the thread.
b) One transforms the path of the thread in a straight axis, with the crossings marked and numbered.
c) One joins the crossings as they are joined in the knot: what crosses at 1, crosses at 4 then 5 etc. The design of the meander reminds us of the labyrinth. .

 

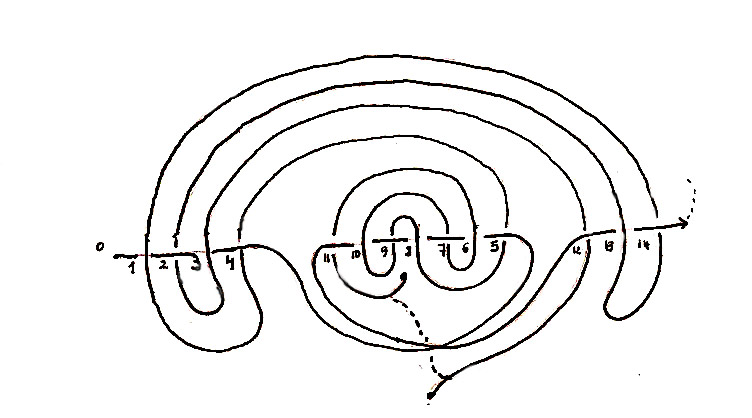
Fig. C

The drawing of the labyrinth when the axis is folded like a snail

 

The two new crossings of the meander where the axis are folded are due to the fact that the observer has turned around the knot. Each time the observer crosses to the other side, one extra crossing is registered. Thus the knot has been charted from all sides. As with Plato’s cave one should thus obtain a more complete and more objective view. The crossing to the other side is also what interrupts the continuity of the meander.

Of course this procedure can seem artificial, but for this mapping of the knot to become logical, it is sufficient to imagine that the knot moves on an orbit. (fig. D).

 

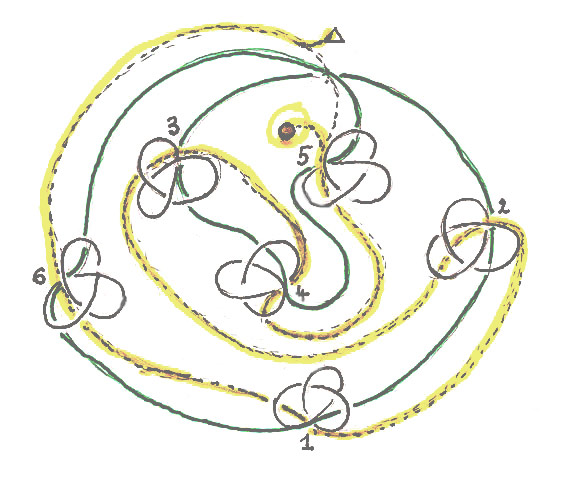
Fig. D

To simplify this demonstration, one uses the simplest knot, which also produces a small labyrinth marked in yellow, but this procedure is the same for the knot with seven crossings.

 

Instead of describing a deconstruction, the drawing of the labyrinth becomes that of a movement. It is surprising to observe the correspondence of an exterior motion and an inner structure. (See 4 Movement).
To obtain the design of the maze one must represent the entire motion of the knot. When the knot spins on itself, as with the earth’s rotation, the maze becomes more complex.

 

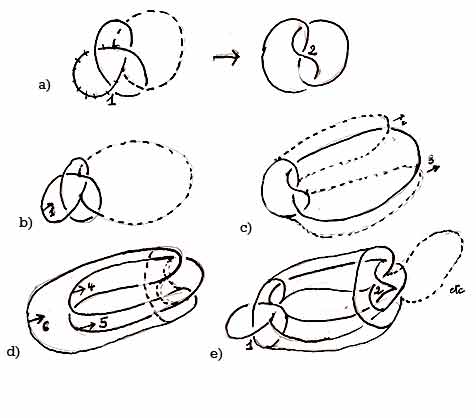
Fig. E

E-a : One can show the spinning of the knot by folding each loop, one after the other. We will again illustrate this with a simple knot. To go from 1 to 2 only one loop topples.
E-b,c,d,e : One must also show the movement of translation of the rest of the knot. The knot with seven crossings produces a more complex figure .

 

The maze can become even more complex. With the example of the simple knot one can conclude that the meander crossing from 1 to 2 can also be considered as crossing at 1 and joining the axis at 5. With this system, or mixing it with the former system, the knot, instead of undoing itself, multiplies itself and becomes infinitely complex. That is why, without the thread of Ariadne, the maze is considered inextricable.

 

 

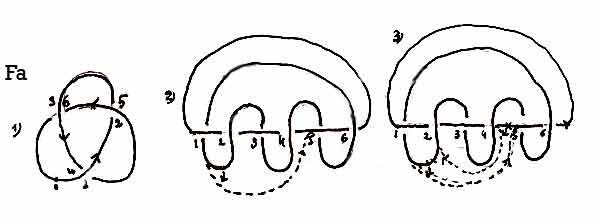
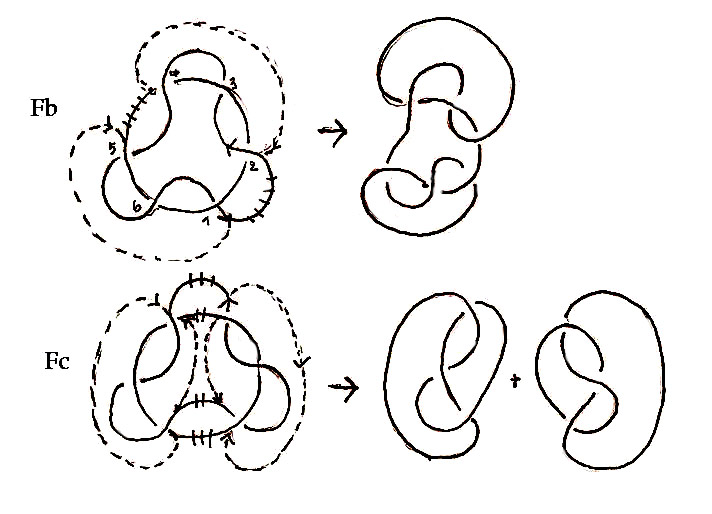
Fig F,a : When one replaces one system with the other, one must also replace the corresponding path of the axis
Fig F,b : If one course is changed, the knot becomes more complex.
Fig F,c : If two courses are changed, two knots, like the original are produced